Unsteady actuator case - 2D

In this example, an unsteady inlet velocity profile at encounters a wind turbine blade in a wall-less domain. The blade is modeled as a uniform body force on a thin rectangle.

Packages

A Makie plotting backend is needed for plotting. GLMakie creates an interactive window (useful for real-time plotting), but does not work when building this example on GitHub. CairoMakie makes high-quality static vector-graphics plots.

julia

using CairoMakie
using IncompressibleNavierStokes

Setup

A 2D grid is a Cartesian product of two vectors

julia

n = 40
x = LinRange(0.0, 10.0, 5n + 1), LinRange(-2.0, 2.0, 2n + 1)
plotgrid(x...; figure = (; size = (600, 300)))

Boundary conditions

julia

inflow(dim, x, y, t) = sinpi(sinpi(t / 6) / 6 + (dim == 1) / 2)
boundary_conditions = ((DirichletBC(inflow), PressureBC()), (PressureBC(), PressureBC()))

((DirichletBC{typeof(Main.inflow)}(Main.inflow), PressureBC()), (PressureBC(), PressureBC()))

Actuator body force: A thrust coefficient Cₜ distributed over a thin rectangle

julia

xc, yc = 2.0, 0.0 # Disk center
D = 1.0           # Disk diameter
δ = 0.11          # Disk thickness
C = 0.2           # Thrust coefficient
c = C / (D * δ)   # Normalize
inside(x, y) = abs(x - xc) ≤ δ / 2 && abs(y - yc) ≤ D / 2
bodyforce(dim, x, y, t) = -c * (dim == 1) * inside(x, y)

bodyforce (generic function with 1 method)

Build setup

julia

setup = Setup(; x, Re = 100.0, boundary_conditions, bodyforce, issteadybodyforce = true);

Initial conditions (extend inflow)

julia

ustart = velocityfield(setup, (dim, x, y) -> inflow(dim, x, y, 0.0))

202×83×2 Array{Float64, 3}:
[:, :, 1] =
 1.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0  …  1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0  …  1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 ⋮                        ⋮              ⋱                      ⋮         
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0  …  1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0  …  1.0  1.0  1.0  1.0  1.0  1.0  1.0
 0.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0     1.0  1.0  1.0  1.0  1.0  1.0  1.0

[:, :, 2] =
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 ⋮                        ⋮              ⋱                      ⋮         
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  …  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0     0.0  0.0  0.0  0.0  0.0  0.0  0.0

Solve unsteady problem

julia

state, outputs = solve_unsteady(;
    setup,
    ustart,
    tlims = (0.0, 12.0),
    method = RKMethods.RK44P2(),
    Δt = 0.05,
    processors = (
        rtp = realtimeplotter(; setup, size = (600, 300), nupdate = 5),
        log = timelogger(; nupdate = 24),
    ),
);

[ Info: t = 1.2	Δt = 0.05	umax = 1.1	itertime = 0.1
[ Info: t = 2.4	Δt = 0.05	umax = 1.1	itertime = 0.038
[ Info: t = 3.6	Δt = 0.05	umax = 1.1	itertime = 0.0087
[ Info: t = 4.8	Δt = 0.05	umax = 1.1	itertime = 0.0094
[ Info: t = 6	Δt = 0.05	umax = 1.1	itertime = 0.0086
[ Info: t = 7.2	Δt = 0.05	umax = 1.1	itertime = 0.0086
[ Info: t = 8.4	Δt = 0.05	umax = 1.1	itertime = 0.0087
[ Info: t = 9.6	Δt = 0.05	umax = 1.1	itertime = 0.0086
[ Info: t = 10.8	Δt = 0.05	umax = 1.1	itertime = 0.0086
[ Info: t = 12	Δt = 0.05	umax = 1.1	itertime = 0.0086

Post-process

We create a box to visualize the actuator.

julia

box = (
    [xc - δ / 2, xc - δ / 2, xc + δ / 2, xc + δ / 2, xc - δ / 2],
    [yc + D / 2, yc - D / 2, yc - D / 2, yc + D / 2, yc + D / 2],
)

([1.945, 1.945, 2.055, 2.055, 1.945], [0.5, -0.5, -0.5, 0.5, 0.5])

Plot pressure

julia

fig = fieldplot(state; setup, size = (600, 300), fieldname = :pressure)
lines!(box...; color = :red)
fig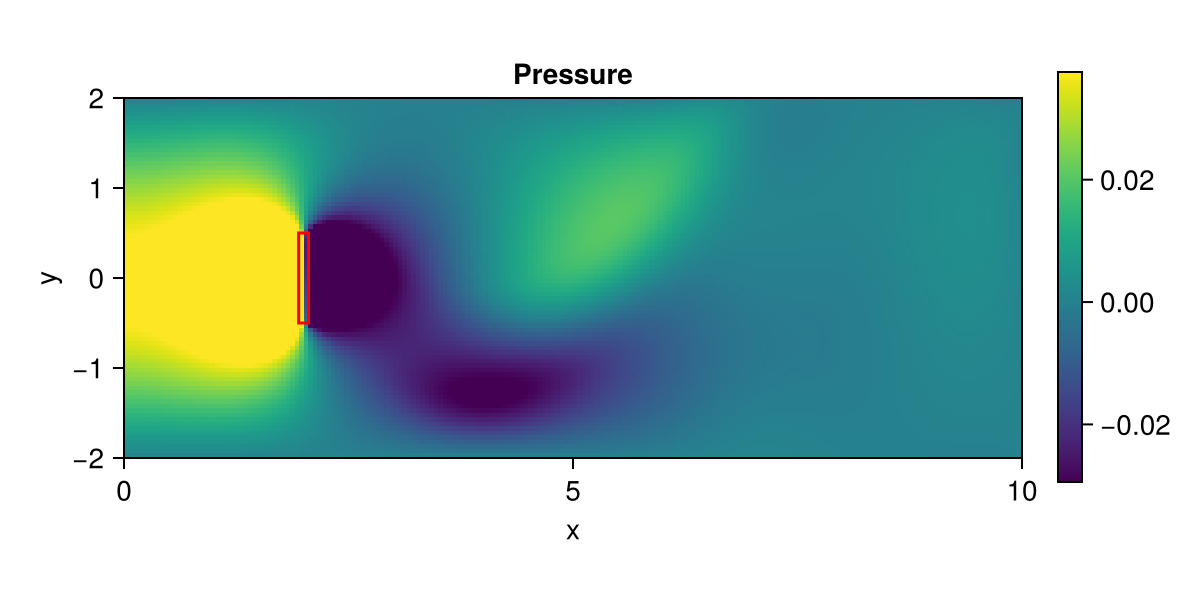

Plot velocity

julia

fig = fieldplot(state; setup, size = (600, 300), fieldname = :velocitynorm)
lines!(box...; color = :red)
fig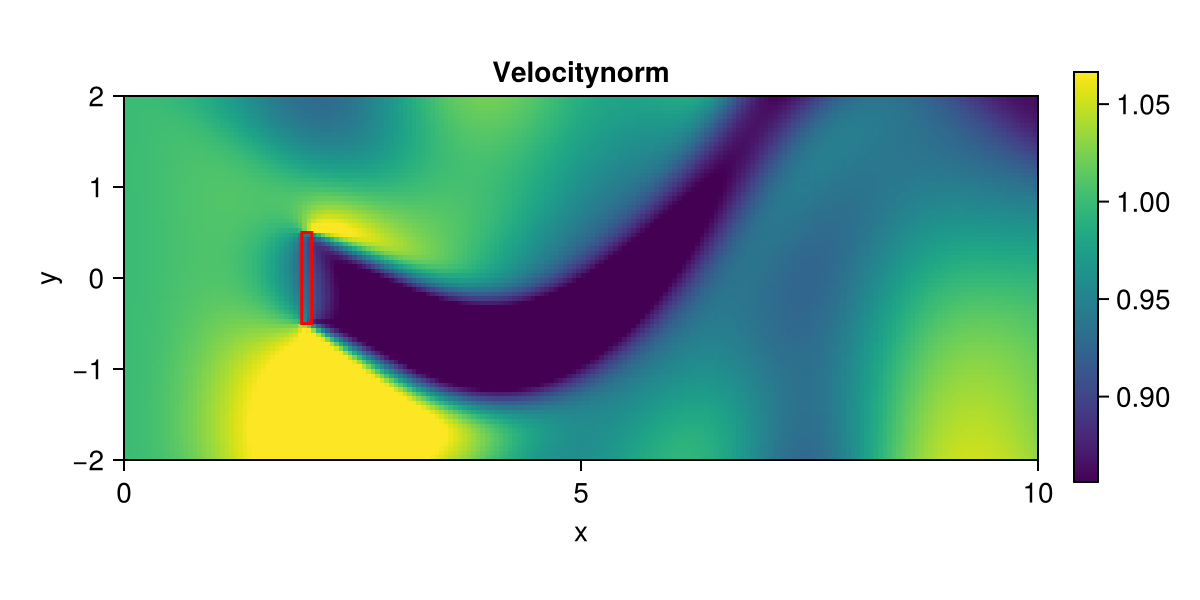

Plot vorticity

julia

fig = fieldplot(state; setup, size = (600, 300), fieldname = :vorticity)
lines!(box...; color = :red)
fig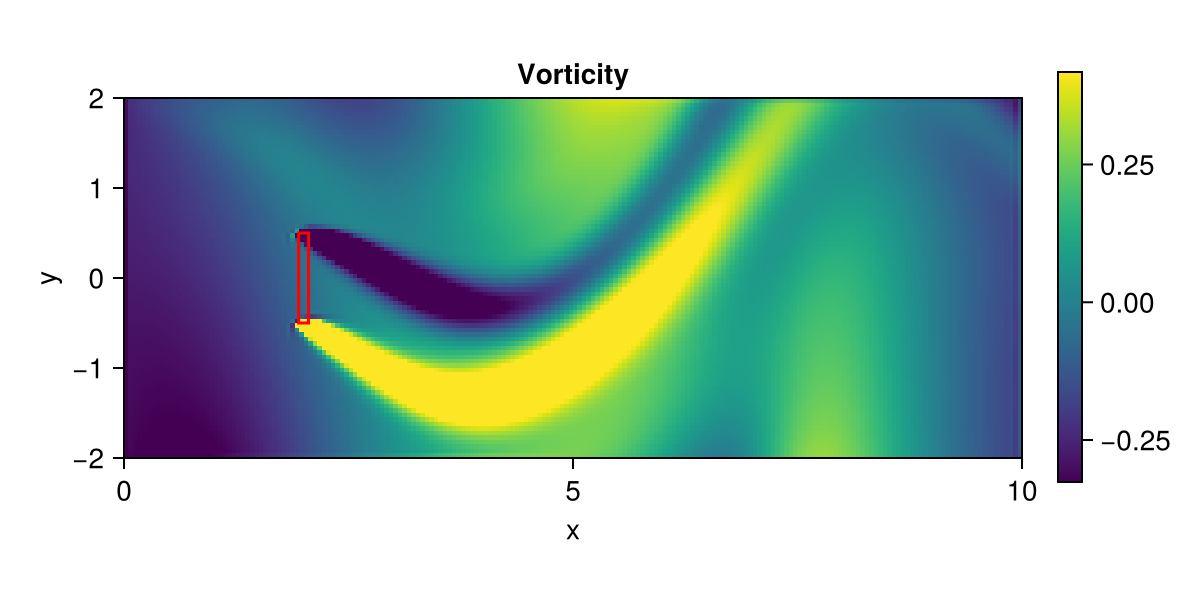

Copy-pasteable code

Below is the full code for this example stripped of comments and output.

julia

using GLMakie
using IncompressibleNavierStokes

n = 40
x = LinRange(0.0, 10.0, 5n + 1), LinRange(-2.0, 2.0, 2n + 1)
plotgrid(x...; figure = (; size = (600, 300)))

inflow(dim, x, y, t) = sinpi(sinpi(t / 6) / 6 + (dim == 1) / 2)
boundary_conditions = ((DirichletBC(inflow), PressureBC()), (PressureBC(), PressureBC()))

xc, yc = 2.0, 0.0 # Disk center
D = 1.0           # Disk diameter
δ = 0.11          # Disk thickness
C = 0.2           # Thrust coefficient
c = C / (D * δ)   # Normalize
inside(x, y) = abs(x - xc) ≤ δ / 2 && abs(y - yc) ≤ D / 2
bodyforce(dim, x, y, t) = -c * (dim == 1) * inside(x, y)

setup = Setup(; x, Re = 100.0, boundary_conditions, bodyforce, issteadybodyforce = true);

ustart = velocityfield(setup, (dim, x, y) -> inflow(dim, x, y, 0.0))

state, outputs = solve_unsteady(;
    setup,
    ustart,
    tlims = (0.0, 12.0),
    method = RKMethods.RK44P2(),
    Δt = 0.05,
    processors = (
        rtp = realtimeplotter(; setup, size = (600, 300), nupdate = 5),
        log = timelogger(; nupdate = 24),
    ),
);

box = (
    [xc - δ / 2, xc - δ / 2, xc + δ / 2, xc + δ / 2, xc - δ / 2],
    [yc + D / 2, yc - D / 2, yc - D / 2, yc + D / 2, yc + D / 2],
)

fig = fieldplot(state; setup, size = (600, 300), fieldname = :pressure)
lines!(box...; color = :red)
fig

fig = fieldplot(state; setup, size = (600, 300), fieldname = :velocitynorm)
lines!(box...; color = :red)
fig

fig = fieldplot(state; setup, size = (600, 300), fieldname = :vorticity)
lines!(box...; color = :red)
fig

This page was generated using Literate.jl.

Unsteady actuator case - 2D ​

Packages ​

Setup ​

Solve unsteady problem ​

Post-process ​

Copy-pasteable code ​

Unsteady actuator case - 2D

Packages

Setup

Solve unsteady problem

Post-process

Copy-pasteable code