Rayleigh-Taylor instability in 2D

Two fluids with different temperatures start mixing.

using CairoMakie
using IncompressibleNavierStokes

Output directory for saving results

outdir = joinpath(@__DIR__, "output", "RayleighTaylor2D")

"/home/runner/work/IncompressibleNavierStokes.jl/IncompressibleNavierStokes.jl/docs/build/examples/generated/output/RayleighTaylor2D"

Hardware

ArrayType = Array

# using CUDA, CUDSS
# ArrayType = CuArray

Array

Precision

T = Float64

Float64

Grid

n = 50
x = tanh_grid(T(0), T(1), n, T(1.5)), tanh_grid(T(0), T(2), 2n, T(1.5))
plotgrid(x...; figure = (; size = (300, 600)))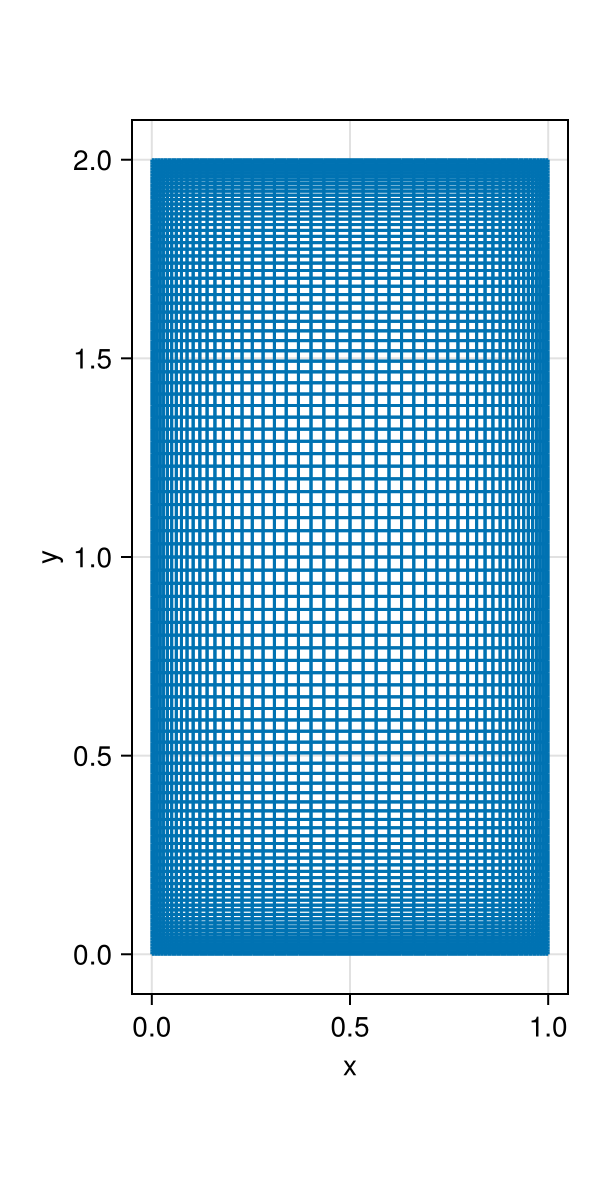

Setup

temperature = temperature_equation(;
    Pr = T(0.71),
    Ra = T(1e6),
    Ge = T(1.0),
    dodissipation = true,
    boundary_conditions = ((SymmetricBC(), SymmetricBC()), (SymmetricBC(), SymmetricBC())),
    gdir = 2,
    nondim_type = 1,
)
setup = Setup(;
    x,
    boundary_conditions = ((DirichletBC(), DirichletBC()), (DirichletBC(), DirichletBC())),
    Re = 1 / temperature.α1,
    temperature,
);

Initial conditions

ustart = velocityfield(setup, (dim, x, y) -> zero(x));
tempstart = temperaturefield(setup, (x, y) -> one(x) * (1 + sinpi(x) / 50 > y));

Solve equation

state, outputs = solve_unsteady(;
    setup,
    ustart,
    tempstart,
    tlims = (T(0), T(10)),
    Δt = T(5e-3),
    processors = (;
        rtp = realtimeplotter(;
            setup,
            nupdate = 20,
            fieldname = :temperature,
            size = (400, 600),
        ),
        log = timelogger(; nupdate = 200),
    ),
);

[ Info: Iteration 200	t = 1	Δt = 0.005	umax = 0.102417
[ Info: Iteration 400	t = 2	Δt = 0.005	umax = 0.324388
[ Info: Iteration 600	t = 3	Δt = 0.005	umax = 0.777547
[ Info: Iteration 800	t = 4	Δt = 0.005	umax = 0.754229
[ Info: Iteration 1000	t = 5	Δt = 0.005	umax = 0.783766
[ Info: Iteration 1200	t = 6	Δt = 0.005	umax = 0.84183
[ Info: Iteration 1400	t = 7	Δt = 0.005	umax = 0.842381
[ Info: Iteration 1600	t = 8	Δt = 0.005	umax = 0.890492
[ Info: Iteration 1800	t = 9	Δt = 0.005	umax = 1.19562
[ Info: Iteration 2000	t = 10	Δt = 0.005	umax = 0.877863

---

This page was generated using Literate.jl.