Unsteady actuator case - 2D

In this example, an unsteady inlet velocity profile at encounters a wind turbine blade in a wall-less domain. The blade is modeled as a uniform body force on a thin rectangle.

We start by loading packages. A Makie plotting backend is needed for plotting. GLMakie creates an interactive window (useful for real-time plotting), but does not work when building this example on GitHub. CairoMakie makes high-quality static vector-graphics plots.

using CairoMakie
using IncompressibleNavierStokes

Output directory

outdir = joinpath(@__DIR__, "output", "Actuator2D")
ispath(outdir) || mkpath(outdir)

"/home/runner/work/IncompressibleNavierStokes.jl/IncompressibleNavierStokes.jl/docs/build/examples/generated/output/Actuator2D"

A 2D grid is a Cartesian product of two vectors

n = 40
x = LinRange(0.0, 10.0, 5n + 1), LinRange(-2.0, 2.0, 2n + 1)
plotgrid(x...; figure = (; size = (600, 300)))

Boundary conditions

boundary_conditions = (
    # x left, x right
    (
        # Unsteady BC requires time derivatives
        DirichletBC((dim, x, y, t) -> sin(π / 6 * sin(π / 6 * t) + π / 2 * (dim == 1))),
        PressureBC(),
    ),

    # y rear, y front
    (PressureBC(), PressureBC()),
)

((DirichletBC{Main.var"#1#2"}(Main.var"#1#2"()), PressureBC()), (PressureBC(), PressureBC()))

Actuator body force: A thrust coefficient Cₜ distributed over a thin rectangle

xc, yc = 2.0, 0.0 # Disk center
D = 1.0           # Disk diameter
δ = 0.11          # Disk thickness
Cₜ = 0.2          # Thrust coefficient
cₜ = Cₜ / (D * δ)
inside(x, y) = abs(x - xc) ≤ δ / 2 && abs(y - yc) ≤ D / 2
bodyforce(dim, x, y, t) = dim == 1 ? -cₜ * inside(x, y) : 0.0

bodyforce (generic function with 1 method)

Build setup and assemble operators

setup = Setup(; x, Re = 100.0, boundary_conditions, bodyforce, issteadybodyforce = true);

Initial conditions (extend inflow)

ustart = velocityfield(setup, (dim, x, y) -> dim == 1 ? 1.0 : 0.0);

Solve unsteady problem

state, outputs = solve_unsteady(;
    setup,
    ustart,
    tlims = (0.0, 12.0),
    method = RKMethods.RK44P2(),
    Δt = 0.05,
    processors = (
        rtp = realtimeplotter(; setup, size = (600, 300), nupdate = 5),
        # ehist = realtimeplotter(; setup, plot = energy_history_plot, nupdate = 1),
        # espec = realtimeplotter(; setup, plot = energy_spectrum_plot, nupdate = 1),
        # anim = animator(;
        #     setup,
        #     path = joinpath(outdir, "solution.mp4"),
        #     size = (600, 300),
        #     nupdate = 5,
        # ),
        # vtk = vtk_writer(; setup, nupdate = 10, dir = "$outdir", filename = "solution"),
        # field = fieldsaver(; setup, nupdate = 10),
        log = timelogger(; nupdate = 24),
    ),
);

[ Info: Iteration 24	t = 1.2	Δt = 0.05	umax = 1.05199
[ Info: Iteration 48	t = 2.4	Δt = 0.05	umax = 1.02356
[ Info: Iteration 72	t = 3.6	Δt = 0.05	umax = 1.01611
[ Info: Iteration 96	t = 4.8	Δt = 0.05	umax = 1.0183
[ Info: Iteration 120	t = 6	Δt = 0.05	umax = 1.02726
[ Info: Iteration 144	t = 7.2	Δt = 0.05	umax = 1.04571
[ Info: Iteration 168	t = 8.4	Δt = 0.05	umax = 1.02813
[ Info: Iteration 192	t = 9.6	Δt = 0.05	umax = 1.03258
[ Info: Iteration 216	t = 10.8	Δt = 0.05	umax = 1.00722
[ Info: Iteration 240	t = 12	Δt = 0.05	umax = 1.02848

Post-process

We may visualize or export the computed fields

Export to VTK

save_vtk(state; setup, filename = joinpath(outdir, "solution"))

1-element Vector{String}:
 "/home/runner/work/Incompressibl" ⋯ 76 bytes ⋯ "/output/Actuator2D/solution.vtr"

We create a box to visualize the actuator.

box = (
    [xc - δ / 2, xc - δ / 2, xc + δ / 2, xc + δ / 2, xc - δ / 2],
    [yc + D / 2, yc - D / 2, yc - D / 2, yc + D / 2, yc + D / 2],
)

([1.945, 1.945, 2.055, 2.055, 1.945], [0.5, -0.5, -0.5, 0.5, 0.5])

Plot pressure

fig = fieldplot(state; setup, size = (600, 300), fieldname = :pressure)
lines!(box...; color = :red)
fig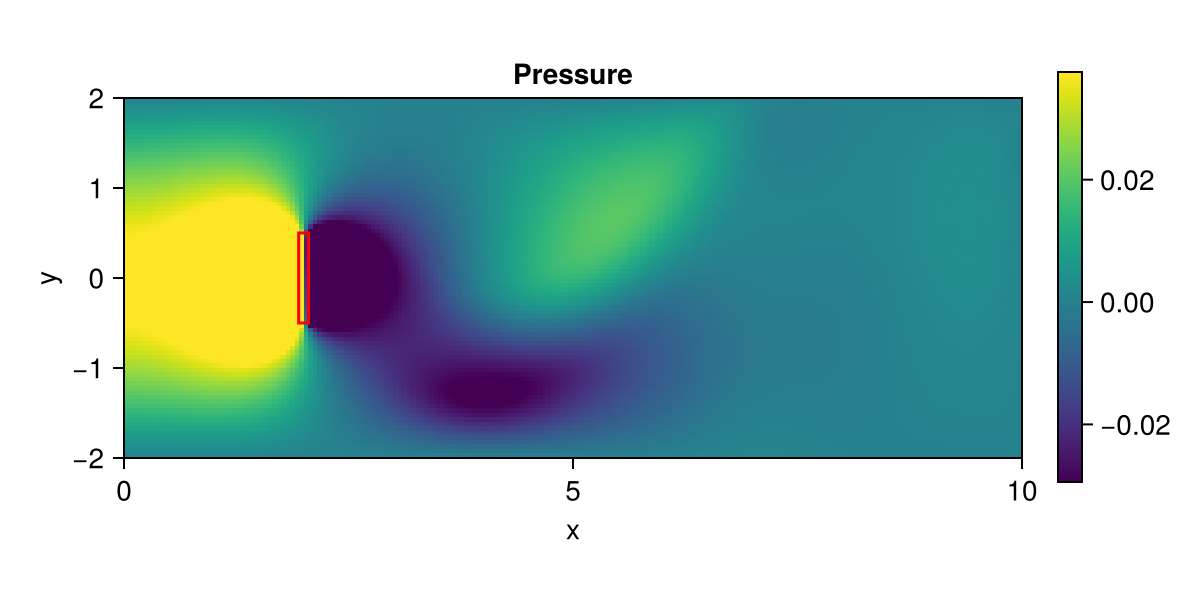

Plot velocity

fig = fieldplot(state; setup, size = (600, 300), fieldname = :velocitynorm)
lines!(box...; color = :red)
fig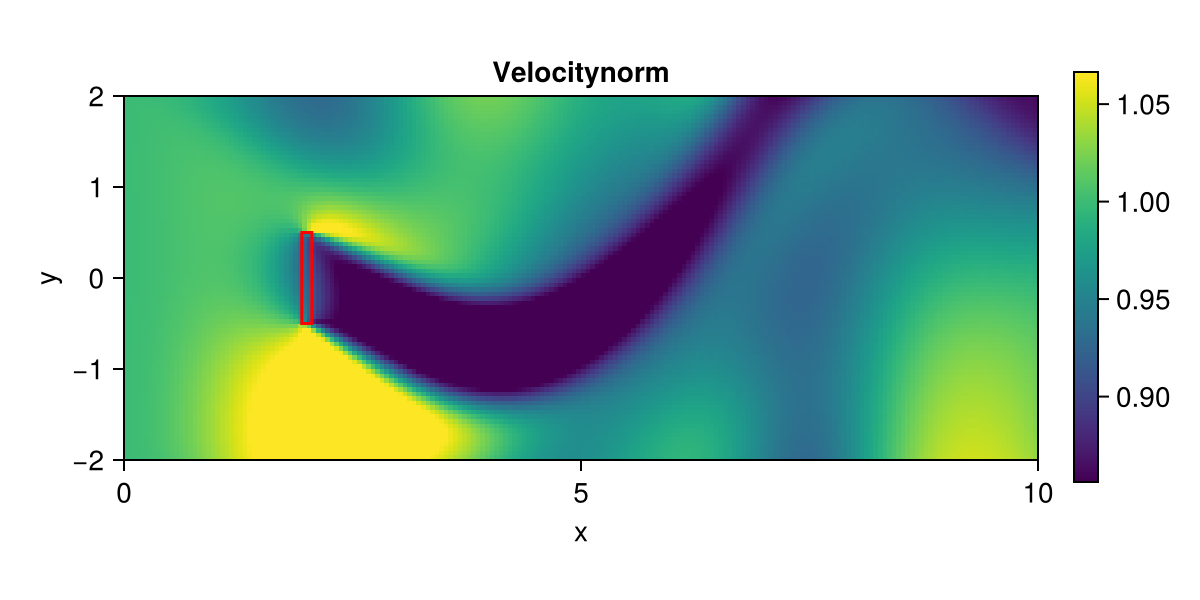

Plot vorticity

fig = fieldplot(state; setup, size = (600, 300), fieldname = :vorticity)
lines!(box...; color = :red)
fig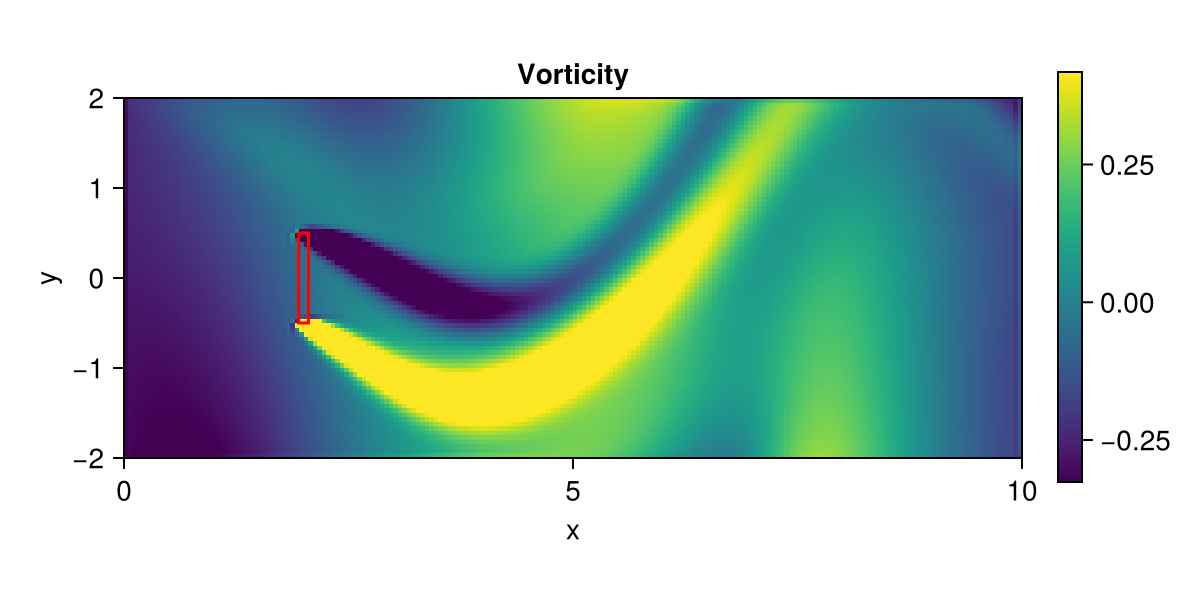

---

This page was generated using Literate.jl.