Rayleigh-Bénard convection (2D)
A hot and a cold plate generate a convection cell in a box.
julia
using CairoMakie
using IncompressibleNavierStokesOutput directory for saving results
julia
outdir = joinpath(@__DIR__, "output", "RayleighBenard2D")"/home/runner/work/IncompressibleNavierStokes.jl/IncompressibleNavierStokes.jl/docs/build/examples/generated/output/RayleighBenard2D"Hardware
julia
backend = CPU()
# using CUDA, CUDSS
# backend = CUDABackend()CPU(false)Define observer function to track Nusselt numbers on top and bottom plates.
julia
function nusseltplot(state; setup)
state isa Observable || (state = Observable(state))
(; Δ, Δu) = setup.grid
Δy1 = Δu[2][1:1] |> sum
Δy2 = Δu[2][end-1:end-1] |> sum
# Observe Nusselt numbers
Nu1 = Observable(Point2f[])
Nu2 = Observable(Point2f[])
on(state) do (; temp, t)
dTdy = @. (temp[:, 2] - temp[:, 1]) / Δy1
Nu = sum((.-dTdy.*Δ[1])[2:end-1])
push!(Nu1[], Point2f(t, Nu))
dTdy = @. (temp[:, end-1] - temp[:, end-2]) / Δy2
Nu = sum((.-dTdy.*Δ[1])[2:end-1])
push!(Nu2[], Point2f(t, Nu))
(Nu1, Nu2) .|> notify ## Update plot
end
# Plot Nu history
fig = Figure()
ax = Axis(fig[1, 1]; title = "Nusselt number", xlabel = "t", ylabel = "Nu")
lines!(ax, Nu1; label = "Lower plate")
lines!(ax, Nu2; label = "Upper plate")
axislegend(ax)
on(_ -> autolimits!(ax), Nu2)
fig
endnusseltplot (generic function with 1 method)Define observer function to track average temperature.
julia
function averagetemp(state; setup)
state isa Observable || (state = Observable(state))
(; xp, Δ, Ip) = setup.grid
ix = Ip.indices[1]
Ty = lift(state) do (; temp)
Ty = sum(temp[ix, :] .* Δ[1][ix]; dims = 1) ./ sum(Δ[1][ix])
Array(Ty)[:]
end
Ty0 = copy(Ty[])
yy = Array(xp[2])
fig = Figure()
ax = Axis(fig[1, 1]; title = "Average temperature", xlabel = "T", ylabel = "y")
lines!(ax, Ty0, yy; label = "t = 0")
lines!(ax, Ty, yy; label = "t = t")
axislegend(ax)
on(_ -> autolimits!(ax), Ty)
fig
endaveragetemp (generic function with 1 method)Instabilities should depend on the floating point precision. Try both Float32 and Float64.
julia
T = Float32Float32Temperature equation setup.
julia
temperature = temperature_equation(;
Pr = T(0.71),
Ra = T(1e7),
Ge = T(1.0),
dodissipation = true,
boundary_conditions = (
(SymmetricBC(), SymmetricBC()),
(DirichletBC(T(1)), DirichletBC(T(0))),
),
gdir = 2,
nondim_type = 1,
)(α1 = 0.00026645826f0, α2 = 1.0f0, α3 = 0.00026645826f0, α4 = 0.0003752933f0, γ = 1.0f0, dodissipation = true, boundary_conditions = ((SymmetricBC(), SymmetricBC()), (DirichletBC{Float32}(1.0f0), DirichletBC{Float32}(0.0f0))), gdir = 2)Grid
julia
n = 100
x = tanh_grid(T(0), T(2), 2n, T(1.2)), tanh_grid(T(0), T(1), n, T(1.2))
plotgrid(x...)
Setup
julia
setup = Setup(;
x,
boundary_conditions = ((DirichletBC(), DirichletBC()), (DirichletBC(), DirichletBC())),
Re = 1 / temperature.α1,
temperature,
backend,
);Initial conditions
julia
ustart = velocityfield(setup, (dim, x, y) -> zero(x));
tempstart = temperaturefield(setup, (x, y) -> one(y) / 2 + max(sinpi(20 * x) / 100, 0));Processors
julia
processors = (;
rtp = realtimeplotter(;
setup,
fieldname = :temperature,
colorrange = (T(0), T(1)),
size = (600, 350),
colormap = :seaborn_icefire_gradient,
nupdate = 20,
),
nusselt = realtimeplotter(;
setup,
plot = nusseltplot,
nupdate = 20,
),
avg = realtimeplotter(;
setup,
plot = averagetemp,
nupdate = 50,
),
log = timelogger(; nupdate = 1000),
)(rtp = (initialize = IncompressibleNavierStokesMakieExt.var"#10#12"{@NamedTuple{grid::@NamedTuple{xlims::Tuple{Tuple{Float32, Float32}, Tuple{Float32, Float32}}, dimension::IncompressibleNavierStokes.Dimension{2}, N::Tuple{Int64, Int64}, Nu::Tuple{Tuple{Int64, Int64}, Tuple{Int64, Int64}}, Np::Tuple{Int64, Int64}, Iu::Tuple{CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}}, Ip::CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, x::Tuple{Vector{Float32}, Vector{Float32}}, xu::Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, xp::Tuple{Vector{Float32}, Vector{Float32}}, Δ::Tuple{Vector{Float32}, Vector{Float32}}, Δu::Tuple{Vector{Float32}, Vector{Float32}}, A::Tuple{Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}}}, boundary_conditions::Tuple{Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}, Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}}, Re::Float32, bodyforce::Nothing, issteadybodyforce::Bool, closure_model::Nothing, backend::CPU, workgroupsize::Int64, temperature::@NamedTuple{α1::Float32, α2::Float32, α3::Float32, α4::Float32, γ::Float32, dodissipation::Bool, boundary_conditions::Tuple{Tuple{SymmetricBC, SymmetricBC}, Tuple{DirichletBC{Float32}, DirichletBC{Float32}}}, gdir::Int64}}, typeof(fieldplot), Int64, Bool, Nothing, Bool, Nothing, Base.Pairs{Symbol, Any, NTuple{4, Symbol}, @NamedTuple{fieldname::Symbol, colorrange::Tuple{Float32, Float32}, size::Tuple{Int64, Int64}, colormap::Symbol}}}((grid = (xlims = ((0.0f0, 2.0f0), (0.0f0, 1.0f0)), dimension = IncompressibleNavierStokes.Dimension{2}(), N = (202, 102), Nu = ((199, 100), (200, 99)), Np = (200, 100), Iu = (CartesianIndices((2:200, 2:101)), CartesianIndices((2:201, 2:100))), Ip = CartesianIndices((2:201, 2:101)), x = (Float32[0.0, 0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0]), xu = ((Float32[0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393, 0.043240547 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679, 0.047299176 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0])), xp = (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), Δ = (Float32[1.1920929f-7, 0.0044347644, 0.0045239925, 0.0046145916, 0.004706502, 0.004799843, 0.004894674, 0.004990816, 0.00508821, 0.005187154 … 0.005187154, 0.00508821, 0.004990816, 0.0048947334, 0.004799843, 0.0047063828, 0.0046145916, 0.0045239925, 0.004434824, 1.1920929f-7], Float32[1.1920929f-7, 0.0044793785, 0.004660547, 0.0048472583, 0.005039513, 0.0052372515, 0.0054405034, 0.005649179, 0.00586316, 0.006082386 … 0.006082356, 0.00586313, 0.005649209, 0.0054404736, 0.0052372813, 0.005039513, 0.004847288, 0.004660487, 0.0044794083, 1.1920929f-7]), Δu = (Float32[0.0022173822, 0.0044793785, 0.004569292, 0.004660547, 0.0047531724, 0.0048472583, 0.004942745, 0.005039513, 0.005137682, 0.0052372515 … 0.005137682, 0.0050395727, 0.004942775, 0.004847288, 0.004753113, 0.004660487, 0.004569292, 0.0044794083, 0.002217412, 1.1920929f-7], Float32[0.0022396892, 0.0045699626, 0.0047539026, 0.0049433857, 0.0051383823, 0.0053388774, 0.0055448413, 0.0057561696, 0.005972773, 0.0061945915 … 0.005972743, 0.0057561994, 0.0055448413, 0.0053389072, 0.005138397, 0.004943371, 0.0047538877, 0.0045699477, 0.0022397041, 1.1920929f-7]), A = (((Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0]), (Float32[1.0, 1.0, 0.5099108, 0.50981885, 0.5097228, 0.50962067, 0.50951755, 0.5094086, 0.50929356, 0.509176 … 0.49093604, 0.49081892, 0.4907065, 0.49058872, 0.4904881, 0.49038374, 0.49028164, 0.49017644, 0.49009407, 0.0], Float32[0.0, 0.49008918, 0.49018115, 0.49027717, 0.49037933, 0.49048245, 0.49059144, 0.49070647, 0.49082395, 0.49094325 … 0.5091811, 0.5092935, 0.5094113, 0.5095119, 0.50961626, 0.50971836, 0.50982356, 0.50990593, 1.0, 1.0])), ((Float32[1.0, 1.0, 0.50497997, 0.50495696, 0.50493026, 0.5049094, 0.5048909, 0.5048628, 0.50483155, 0.5048146 … 0.49520862, 0.4951738, 0.4951626, 0.49514025, 0.49510598, 0.4950843, 0.49507612, 0.49504304, 0.49502343, 0.0], Float32[0.0, 0.49502006, 0.49504304, 0.49506977, 0.4950906, 0.49510905, 0.4951372, 0.49516848, 0.4951854, 0.49521717 … 0.5048262, 0.5048374, 0.50485975, 0.504894, 0.5049157, 0.5049239, 0.50495696, 0.5049766, 1.0, 1.0]), (Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0])))), boundary_conditions = ((DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing)), (DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing))), Re = 3752.933f0, bodyforce = nothing, issteadybodyforce = false, closure_model = nothing, backend = CPU(false), workgroupsize = 64, temperature = (α1 = 0.00026645826f0, α2 = 1.0f0, α3 = 0.00026645826f0, α4 = 0.0003752933f0, γ = 1.0f0, dodissipation = true, boundary_conditions = ((SymmetricBC(), SymmetricBC()), (DirichletBC{Float32}(1.0f0), DirichletBC{Float32}(0.0f0))), gdir = 2)), IncompressibleNavierStokes.fieldplot, 20, true, nothing, false, nothing, Base.Pairs{Symbol, Any, NTuple{4, Symbol}, @NamedTuple{fieldname::Symbol, colorrange::Tuple{Float32, Float32}, size::Tuple{Int64, Int64}, colormap::Symbol}}(:fieldname => :temperature, :colorrange => (0.0f0, 1.0f0), :size => (600, 350), :colormap => :seaborn_icefire_gradient)), finalize = IncompressibleNavierStokes.var"#295#296"()), nusselt = (initialize = IncompressibleNavierStokesMakieExt.var"#10#12"{@NamedTuple{grid::@NamedTuple{xlims::Tuple{Tuple{Float32, Float32}, Tuple{Float32, Float32}}, dimension::IncompressibleNavierStokes.Dimension{2}, N::Tuple{Int64, Int64}, Nu::Tuple{Tuple{Int64, Int64}, Tuple{Int64, Int64}}, Np::Tuple{Int64, Int64}, Iu::Tuple{CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}}, Ip::CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, x::Tuple{Vector{Float32}, Vector{Float32}}, xu::Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, xp::Tuple{Vector{Float32}, Vector{Float32}}, Δ::Tuple{Vector{Float32}, Vector{Float32}}, Δu::Tuple{Vector{Float32}, Vector{Float32}}, A::Tuple{Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}}}, boundary_conditions::Tuple{Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}, Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}}, Re::Float32, bodyforce::Nothing, issteadybodyforce::Bool, closure_model::Nothing, backend::CPU, workgroupsize::Int64, temperature::@NamedTuple{α1::Float32, α2::Float32, α3::Float32, α4::Float32, γ::Float32, dodissipation::Bool, boundary_conditions::Tuple{Tuple{SymmetricBC, SymmetricBC}, Tuple{DirichletBC{Float32}, DirichletBC{Float32}}}, gdir::Int64}}, typeof(Main.nusseltplot), Int64, Bool, Nothing, Bool, Nothing, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}}((grid = (xlims = ((0.0f0, 2.0f0), (0.0f0, 1.0f0)), dimension = IncompressibleNavierStokes.Dimension{2}(), N = (202, 102), Nu = ((199, 100), (200, 99)), Np = (200, 100), Iu = (CartesianIndices((2:200, 2:101)), CartesianIndices((2:201, 2:100))), Ip = CartesianIndices((2:201, 2:101)), x = (Float32[0.0, 0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0]), xu = ((Float32[0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393, 0.043240547 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679, 0.047299176 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0])), xp = (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), Δ = (Float32[1.1920929f-7, 0.0044347644, 0.0045239925, 0.0046145916, 0.004706502, 0.004799843, 0.004894674, 0.004990816, 0.00508821, 0.005187154 … 0.005187154, 0.00508821, 0.004990816, 0.0048947334, 0.004799843, 0.0047063828, 0.0046145916, 0.0045239925, 0.004434824, 1.1920929f-7], Float32[1.1920929f-7, 0.0044793785, 0.004660547, 0.0048472583, 0.005039513, 0.0052372515, 0.0054405034, 0.005649179, 0.00586316, 0.006082386 … 0.006082356, 0.00586313, 0.005649209, 0.0054404736, 0.0052372813, 0.005039513, 0.004847288, 0.004660487, 0.0044794083, 1.1920929f-7]), Δu = (Float32[0.0022173822, 0.0044793785, 0.004569292, 0.004660547, 0.0047531724, 0.0048472583, 0.004942745, 0.005039513, 0.005137682, 0.0052372515 … 0.005137682, 0.0050395727, 0.004942775, 0.004847288, 0.004753113, 0.004660487, 0.004569292, 0.0044794083, 0.002217412, 1.1920929f-7], Float32[0.0022396892, 0.0045699626, 0.0047539026, 0.0049433857, 0.0051383823, 0.0053388774, 0.0055448413, 0.0057561696, 0.005972773, 0.0061945915 … 0.005972743, 0.0057561994, 0.0055448413, 0.0053389072, 0.005138397, 0.004943371, 0.0047538877, 0.0045699477, 0.0022397041, 1.1920929f-7]), A = (((Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0]), (Float32[1.0, 1.0, 0.5099108, 0.50981885, 0.5097228, 0.50962067, 0.50951755, 0.5094086, 0.50929356, 0.509176 … 0.49093604, 0.49081892, 0.4907065, 0.49058872, 0.4904881, 0.49038374, 0.49028164, 0.49017644, 0.49009407, 0.0], Float32[0.0, 0.49008918, 0.49018115, 0.49027717, 0.49037933, 0.49048245, 0.49059144, 0.49070647, 0.49082395, 0.49094325 … 0.5091811, 0.5092935, 0.5094113, 0.5095119, 0.50961626, 0.50971836, 0.50982356, 0.50990593, 1.0, 1.0])), ((Float32[1.0, 1.0, 0.50497997, 0.50495696, 0.50493026, 0.5049094, 0.5048909, 0.5048628, 0.50483155, 0.5048146 … 0.49520862, 0.4951738, 0.4951626, 0.49514025, 0.49510598, 0.4950843, 0.49507612, 0.49504304, 0.49502343, 0.0], Float32[0.0, 0.49502006, 0.49504304, 0.49506977, 0.4950906, 0.49510905, 0.4951372, 0.49516848, 0.4951854, 0.49521717 … 0.5048262, 0.5048374, 0.50485975, 0.504894, 0.5049157, 0.5049239, 0.50495696, 0.5049766, 1.0, 1.0]), (Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0])))), boundary_conditions = ((DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing)), (DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing))), Re = 3752.933f0, bodyforce = nothing, issteadybodyforce = false, closure_model = nothing, backend = CPU(false), workgroupsize = 64, temperature = (α1 = 0.00026645826f0, α2 = 1.0f0, α3 = 0.00026645826f0, α4 = 0.0003752933f0, γ = 1.0f0, dodissipation = true, boundary_conditions = ((SymmetricBC(), SymmetricBC()), (DirichletBC{Float32}(1.0f0), DirichletBC{Float32}(0.0f0))), gdir = 2)), Main.nusseltplot, 20, true, nothing, false, nothing, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}()), finalize = IncompressibleNavierStokes.var"#295#296"()), avg = (initialize = IncompressibleNavierStokesMakieExt.var"#10#12"{@NamedTuple{grid::@NamedTuple{xlims::Tuple{Tuple{Float32, Float32}, Tuple{Float32, Float32}}, dimension::IncompressibleNavierStokes.Dimension{2}, N::Tuple{Int64, Int64}, Nu::Tuple{Tuple{Int64, Int64}, Tuple{Int64, Int64}}, Np::Tuple{Int64, Int64}, Iu::Tuple{CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}}, Ip::CartesianIndices{2, Tuple{UnitRange{Int64}, UnitRange{Int64}}}, x::Tuple{Vector{Float32}, Vector{Float32}}, xu::Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, xp::Tuple{Vector{Float32}, Vector{Float32}}, Δ::Tuple{Vector{Float32}, Vector{Float32}}, Δu::Tuple{Vector{Float32}, Vector{Float32}}, A::Tuple{Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}, Tuple{Tuple{Vector{Float32}, Vector{Float32}}, Tuple{Vector{Float32}, Vector{Float32}}}}}, boundary_conditions::Tuple{Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}, Tuple{DirichletBC{Nothing}, DirichletBC{Nothing}}}, Re::Float32, bodyforce::Nothing, issteadybodyforce::Bool, closure_model::Nothing, backend::CPU, workgroupsize::Int64, temperature::@NamedTuple{α1::Float32, α2::Float32, α3::Float32, α4::Float32, γ::Float32, dodissipation::Bool, boundary_conditions::Tuple{Tuple{SymmetricBC, SymmetricBC}, Tuple{DirichletBC{Float32}, DirichletBC{Float32}}}, gdir::Int64}}, typeof(Main.averagetemp), Int64, Bool, Nothing, Bool, Nothing, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}}((grid = (xlims = ((0.0f0, 2.0f0), (0.0f0, 1.0f0)), dimension = IncompressibleNavierStokes.Dimension{2}(), N = (202, 102), Nu = ((199, 100), (200, 99)), Np = (200, 100), Iu = (CartesianIndices((2:200, 2:101)), CartesianIndices((2:201, 2:100))), Ip = CartesianIndices((2:201, 2:101)), x = (Float32[0.0, 0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0]), xu = ((Float32[0.0, 0.0044347644, 0.008958757, 0.0135733485, 0.01827985, 0.023079693, 0.027974367, 0.032965183, 0.038053393, 0.043240547 … 1.9619466, 1.9670348, 1.9720256, 1.9769204, 1.9817202, 1.9864266, 1.9910412, 1.9955652, 2.0, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0044793785, 0.009139925, 0.013987184, 0.019026697, 0.024263948, 0.029704452, 0.03535363, 0.04121679, 0.047299176 … 0.9587832, 0.96464634, 0.97029555, 0.975736, 0.9809733, 0.9860128, 0.9908601, 0.9955206, 1.0, 1.0])), xp = (Float32[0.0, 0.0022173822, 0.0066967607, 0.011266053, 0.0159266, 0.020679772, 0.02552703, 0.030469775, 0.03550929, 0.04064697 … 1.959353, 1.9644907, 1.9695302, 1.974473, 1.9793203, 1.9840734, 1.9887339, 1.9933032, 1.9977826, 2.0], Float32[0.0, 0.0022396892, 0.006809652, 0.011563554, 0.01650694, 0.021645322, 0.0269842, 0.03252904, 0.03828521, 0.044257984 … 0.955742, 0.96171474, 0.96747094, 0.9730158, 0.9783547, 0.9834931, 0.98843646, 0.99319035, 0.9977603, 1.0]), Δ = (Float32[1.1920929f-7, 0.0044347644, 0.0045239925, 0.0046145916, 0.004706502, 0.004799843, 0.004894674, 0.004990816, 0.00508821, 0.005187154 … 0.005187154, 0.00508821, 0.004990816, 0.0048947334, 0.004799843, 0.0047063828, 0.0046145916, 0.0045239925, 0.004434824, 1.1920929f-7], Float32[1.1920929f-7, 0.0044793785, 0.004660547, 0.0048472583, 0.005039513, 0.0052372515, 0.0054405034, 0.005649179, 0.00586316, 0.006082386 … 0.006082356, 0.00586313, 0.005649209, 0.0054404736, 0.0052372813, 0.005039513, 0.004847288, 0.004660487, 0.0044794083, 1.1920929f-7]), Δu = (Float32[0.0022173822, 0.0044793785, 0.004569292, 0.004660547, 0.0047531724, 0.0048472583, 0.004942745, 0.005039513, 0.005137682, 0.0052372515 … 0.005137682, 0.0050395727, 0.004942775, 0.004847288, 0.004753113, 0.004660487, 0.004569292, 0.0044794083, 0.002217412, 1.1920929f-7], Float32[0.0022396892, 0.0045699626, 0.0047539026, 0.0049433857, 0.0051383823, 0.0053388774, 0.0055448413, 0.0057561696, 0.005972773, 0.0061945915 … 0.005972743, 0.0057561994, 0.0055448413, 0.0053389072, 0.005138397, 0.004943371, 0.0047538877, 0.0045699477, 0.0022397041, 1.1920929f-7]), A = (((Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0]), (Float32[1.0, 1.0, 0.5099108, 0.50981885, 0.5097228, 0.50962067, 0.50951755, 0.5094086, 0.50929356, 0.509176 … 0.49093604, 0.49081892, 0.4907065, 0.49058872, 0.4904881, 0.49038374, 0.49028164, 0.49017644, 0.49009407, 0.0], Float32[0.0, 0.49008918, 0.49018115, 0.49027717, 0.49037933, 0.49048245, 0.49059144, 0.49070647, 0.49082395, 0.49094325 … 0.5091811, 0.5092935, 0.5094113, 0.5095119, 0.50961626, 0.50971836, 0.50982356, 0.50990593, 1.0, 1.0])), ((Float32[1.0, 1.0, 0.50497997, 0.50495696, 0.50493026, 0.5049094, 0.5048909, 0.5048628, 0.50483155, 0.5048146 … 0.49520862, 0.4951738, 0.4951626, 0.49514025, 0.49510598, 0.4950843, 0.49507612, 0.49504304, 0.49502343, 0.0], Float32[0.0, 0.49502006, 0.49504304, 0.49506977, 0.4950906, 0.49510905, 0.4951372, 0.49516848, 0.4951854, 0.49521717 … 0.5048262, 0.5048374, 0.50485975, 0.504894, 0.5049157, 0.5049239, 0.50495696, 0.5049766, 1.0, 1.0]), (Float32[1.0, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5], Float32[0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 … 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0])))), boundary_conditions = ((DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing)), (DirichletBC{Nothing}(nothing), DirichletBC{Nothing}(nothing))), Re = 3752.933f0, bodyforce = nothing, issteadybodyforce = false, closure_model = nothing, backend = CPU(false), workgroupsize = 64, temperature = (α1 = 0.00026645826f0, α2 = 1.0f0, α3 = 0.00026645826f0, α4 = 0.0003752933f0, γ = 1.0f0, dodissipation = true, boundary_conditions = ((SymmetricBC(), SymmetricBC()), (DirichletBC{Float32}(1.0f0), DirichletBC{Float32}(0.0f0))), gdir = 2)), Main.averagetemp, 50, true, nothing, false, nothing, Base.Pairs{Symbol, Union{}, Tuple{}, @NamedTuple{}}()), finalize = IncompressibleNavierStokes.var"#295#296"()), log = (initialize = IncompressibleNavierStokes.var"#298#300"{Bool, Bool, Bool, Bool, Bool, Int64}(false, true, true, true, true, 1000), finalize = IncompressibleNavierStokes.var"#295#296"()))Solve equation
julia
state, outputs = solve_unsteady(;
setup,
ustart,
tempstart,
tlims = (T(0), T(20)),
Δt = T(1e-2),
processors,
);[ Info: t = 10.0001 Δt = 0.01 umax = 0.24 itertime = 0.014
[ Info: t = 20.0004 Δt = 0.01 umax = 0.55 itertime = 0.012Nusselt numbers
julia
outputs.nusselt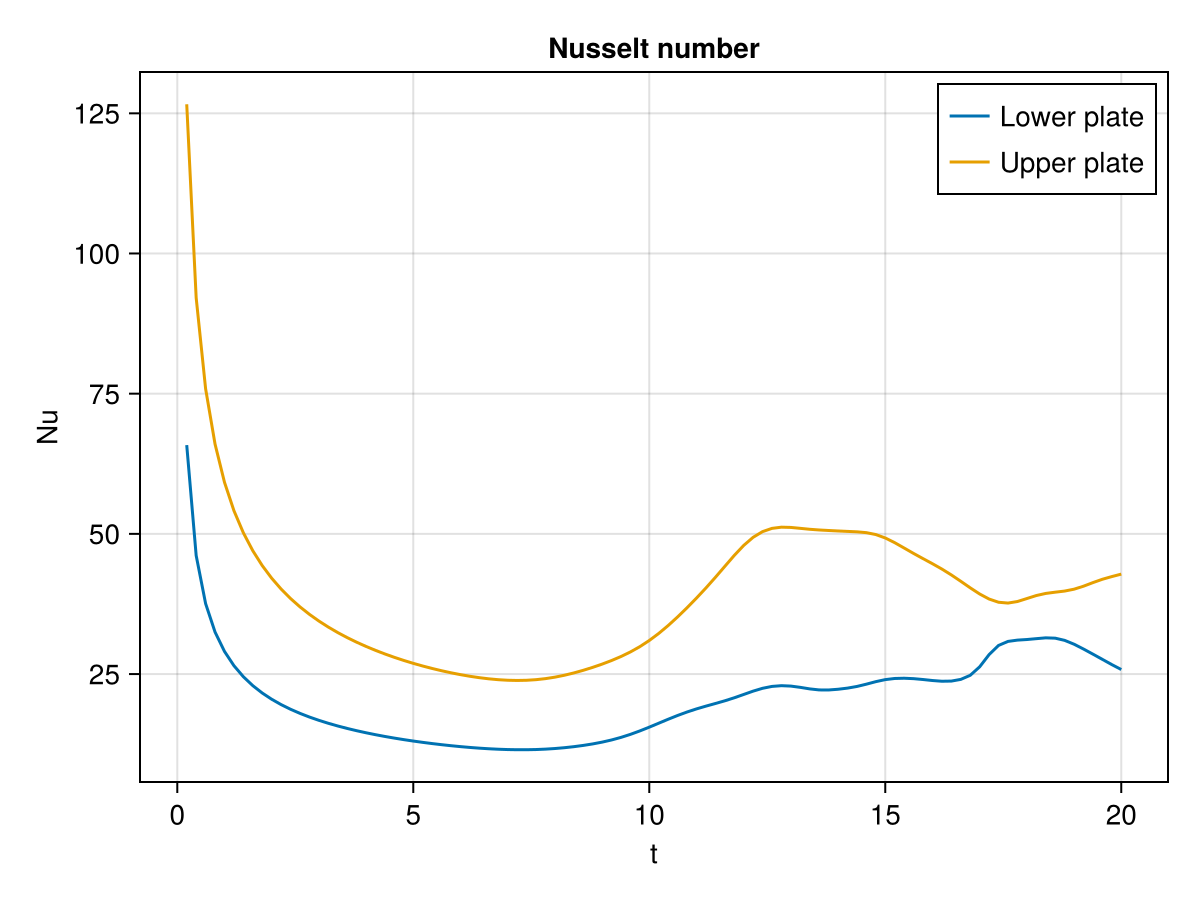
Average temperature
julia
outputs.avg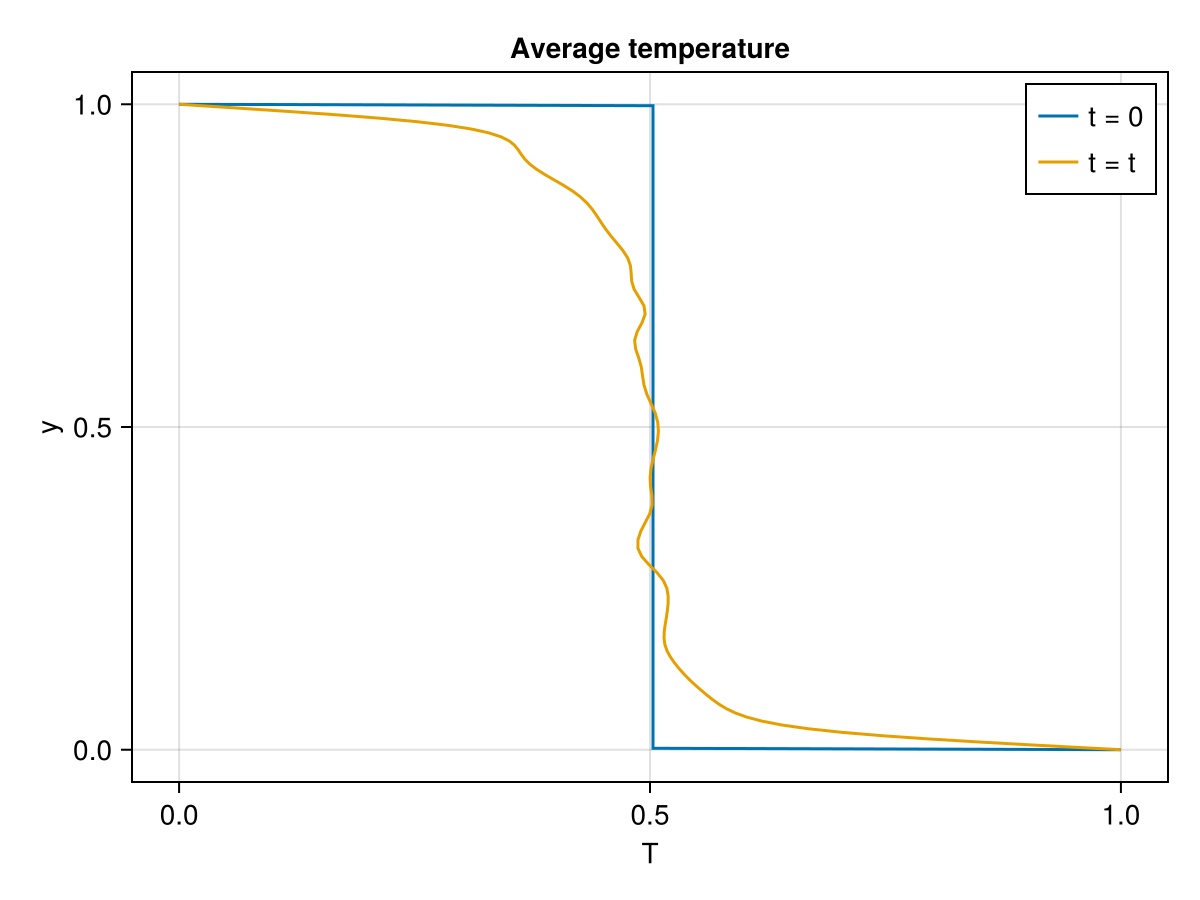
Copy-pasteable code
Below is the full code for this example stripped of comments and output.
julia
using GLMakie
using IncompressibleNavierStokes
outdir = joinpath(@__DIR__, "output", "RayleighBenard2D")
backend = CPU()
# using CUDA, CUDSS
# backend = CUDABackend()
function nusseltplot(state; setup)
state isa Observable || (state = Observable(state))
(; Δ, Δu) = setup.grid
Δy1 = Δu[2][1:1] |> sum
Δy2 = Δu[2][end-1:end-1] |> sum
# Observe Nusselt numbers
Nu1 = Observable(Point2f[])
Nu2 = Observable(Point2f[])
on(state) do (; temp, t)
dTdy = @. (temp[:, 2] - temp[:, 1]) / Δy1
Nu = sum((.-dTdy.*Δ[1])[2:end-1])
push!(Nu1[], Point2f(t, Nu))
dTdy = @. (temp[:, end-1] - temp[:, end-2]) / Δy2
Nu = sum((.-dTdy.*Δ[1])[2:end-1])
push!(Nu2[], Point2f(t, Nu))
(Nu1, Nu2) .|> notify ## Update plot
end
# Plot Nu history
fig = Figure()
ax = Axis(fig[1, 1]; title = "Nusselt number", xlabel = "t", ylabel = "Nu")
lines!(ax, Nu1; label = "Lower plate")
lines!(ax, Nu2; label = "Upper plate")
axislegend(ax)
on(_ -> autolimits!(ax), Nu2)
fig
end
function averagetemp(state; setup)
state isa Observable || (state = Observable(state))
(; xp, Δ, Ip) = setup.grid
ix = Ip.indices[1]
Ty = lift(state) do (; temp)
Ty = sum(temp[ix, :] .* Δ[1][ix]; dims = 1) ./ sum(Δ[1][ix])
Array(Ty)[:]
end
Ty0 = copy(Ty[])
yy = Array(xp[2])
fig = Figure()
ax = Axis(fig[1, 1]; title = "Average temperature", xlabel = "T", ylabel = "y")
lines!(ax, Ty0, yy; label = "t = 0")
lines!(ax, Ty, yy; label = "t = t")
axislegend(ax)
on(_ -> autolimits!(ax), Ty)
fig
end
T = Float32
temperature = temperature_equation(;
Pr = T(0.71),
Ra = T(1e7),
Ge = T(1.0),
dodissipation = true,
boundary_conditions = (
(SymmetricBC(), SymmetricBC()),
(DirichletBC(T(1)), DirichletBC(T(0))),
),
gdir = 2,
nondim_type = 1,
)
n = 100
x = tanh_grid(T(0), T(2), 2n, T(1.2)), tanh_grid(T(0), T(1), n, T(1.2))
plotgrid(x...)
setup = Setup(;
x,
boundary_conditions = ((DirichletBC(), DirichletBC()), (DirichletBC(), DirichletBC())),
Re = 1 / temperature.α1,
temperature,
backend,
);
ustart = velocityfield(setup, (dim, x, y) -> zero(x));
tempstart = temperaturefield(setup, (x, y) -> one(y) / 2 + max(sinpi(20 * x) / 100, 0));
GLMakie.closeall()
processors = (;
rtp = realtimeplotter(;
screen = GLMakie.Screen(),
setup,
fieldname = :temperature,
colorrange = (T(0), T(1)),
size = (600, 350),
colormap = :seaborn_icefire_gradient,
nupdate = 20,
),
nusselt = realtimeplotter(;
screen = GLMakie.Screen(),
setup,
plot = nusseltplot,
nupdate = 20,
),
avg = realtimeplotter(;
screen = GLMakie.Screen(),
setup,
plot = averagetemp,
nupdate = 50,
),
log = timelogger(; nupdate = 1000),
)
state, outputs = solve_unsteady(;
setup,
ustart,
tempstart,
tlims = (T(0), T(20)),
Δt = T(1e-2),
processors,
);
outputs.nusselt
outputs.avgThis page was generated using Literate.jl.