Convergence study: Taylor-Green vortex (2D)

In this example we consider the Taylor-Green vortex. In 2D, it has an analytical solution, given by

$$\begin{array}{rl}{u}^1(x,y,t)& =-\sin (x)\cos (y){\mathrm{e}}^{-2t/Re}\\ u^2(x,y,t)& =+\cos (x)\sin (y){\mathrm{e}}^{-2t/Re}\end{array}$$

This allows us to test the convergence of our solver.

using CairoMakie
using IncompressibleNavierStokes
using LinearAlgebra

Output directory

outdir = joinpath(@__DIR__, "output", "TaylorGreenVortex2D")
ispath(outdir) || mkpath(outdir)

"/home/runner/work/IncompressibleNavierStokes.jl/IncompressibleNavierStokes.jl/docs/build/examples/generated/output/TaylorGreenVortex2D"

Convergence

"""
Compare numerical solution with analytical solution at final time.
"""
function compute_convergence(; D, nlist, lims, Re, tlims, Δt, uref, backend = CPU())
    T = typeof(lims[1])
    e = zeros(T, length(nlist))
    for (i, n) in enumerate(nlist)
        @info "Computing error for n = $n"
        x = ntuple(α -> LinRange(lims..., n + 1), D)
        setup = Setup(; x, Re, backend)
        psolver = psolver_spectral(setup)
        ustart = velocityfield(
            setup,
            (dim, x...) -> uref(dim, x..., tlims[1]),
            tlims[1];
            psolver,
        )
        ut = velocityfield(
            setup,
            (dim, x...) -> uref(dim, x..., tlims[2]),
            tlims[2];
            psolver,
            doproject = false,
        )
        (; u, t), outputs = solve_unsteady(; setup, ustart, tlims, Δt, psolver)
        (; Ip) = setup.grid
        a = sum(abs2, u[Ip, :] - ut[Ip, :])
        b = sum(abs2, ut[Ip, :])
        e[i] = sqrt(a) / sqrt(b)
    end
    e
end

Main.compute_convergence

Analytical solution for 2D Taylor-Green vortex

solution(Re) =
    (dim, x, y, t) -> (dim == 1 ? -sin(x) * cos(y) : cos(x) * sin(y)) * exp(-2t / Re)

solution (generic function with 1 method)

Compute error for different resolutions

Re = 2.0e3
nlist = [2, 4, 8, 16, 32, 64, 128, 256]
e = compute_convergence(;
    D = 2,
    nlist,
    lims = (0.0, 2π),
    Re,
    tlims = (0.0, 2.0),
    Δt = 0.01,
    uref = solution(Re),
)

8-element Vector{Float64}:
 0.4242656052086717
 0.000378932838635171
 0.0001007226650833037
 2.5570665390686788e-5
 6.417292500615618e-6
 1.6058662108882434e-6
 4.01563057410408e-7
 1.003967967340085e-7

Plot convergence

fig = Figure()
ax = Axis(
    fig[1, 1];
    xscale = log10,
    yscale = log10,
    xticks = nlist,
    xlabel = "n",
    title = "Relative error",
)
scatterlines!(ax, nlist, e; label = "Data")
lines!(ax, collect(extrema(nlist)), n -> n^-2.0; linestyle = :dash, label = "n^-2")
axislegend(ax)
fig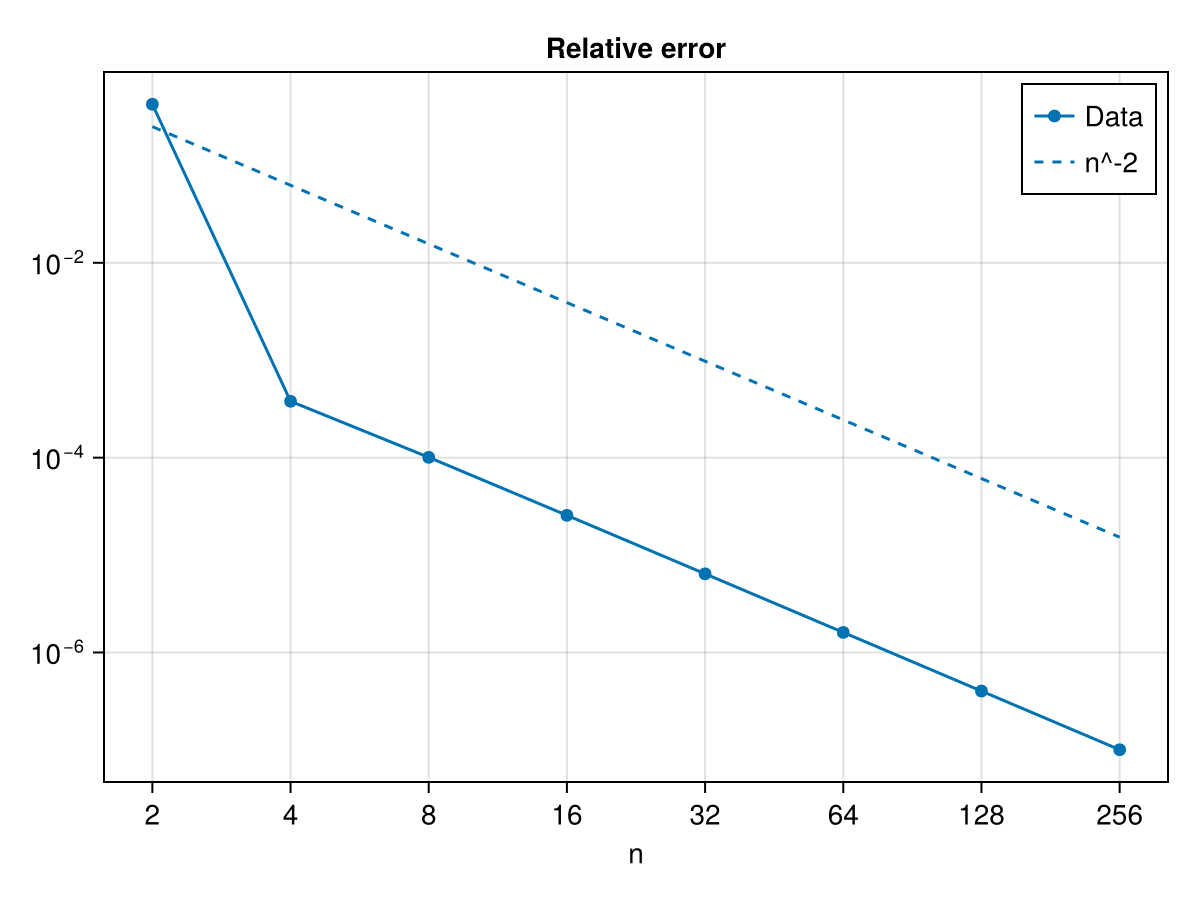

Save figure

save(joinpath(outdir, "convergence.png"), fig)

CairoMakie.Screen{IMAGE}

Copy-pasteable code

Below is the full code for this example stripped of comments and output.

using GLMakie
using IncompressibleNavierStokes
using LinearAlgebra

outdir = joinpath(@__DIR__, "output", "TaylorGreenVortex2D")
ispath(outdir) || mkpath(outdir)

"""
Compare numerical solution with analytical solution at final time.
"""
function compute_convergence(; D, nlist, lims, Re, tlims, Δt, uref, backend = CPU())
    T = typeof(lims[1])
    e = zeros(T, length(nlist))
    for (i, n) in enumerate(nlist)
        @info "Computing error for n = $n"
        x = ntuple(α -> LinRange(lims..., n + 1), D)
        setup = Setup(; x, Re, backend)
        psolver = psolver_spectral(setup)
        ustart = velocityfield(
            setup,
            (dim, x...) -> uref(dim, x..., tlims[1]),
            tlims[1];
            psolver,
        )
        ut = velocityfield(
            setup,
            (dim, x...) -> uref(dim, x..., tlims[2]),
            tlims[2];
            psolver,
            doproject = false,
        )
        (; u, t), outputs = solve_unsteady(; setup, ustart, tlims, Δt, psolver)
        (; Ip) = setup.grid
        a = sum(abs2, u[Ip, :] - ut[Ip, :])
        b = sum(abs2, ut[Ip, :])
        e[i] = sqrt(a) / sqrt(b)
    end
    e
end

solution(Re) =
    (dim, x, y, t) -> (dim == 1 ? -sin(x) * cos(y) : cos(x) * sin(y)) * exp(-2t / Re)

Re = 2.0e3
nlist = [2, 4, 8, 16, 32, 64, 128, 256]
e = compute_convergence(;
    D = 2,
    nlist,
    lims = (0.0, 2π),
    Re,
    tlims = (0.0, 2.0),
    Δt = 0.01,
    uref = solution(Re),
)

fig = Figure()
ax = Axis(
    fig[1, 1];
    xscale = log10,
    yscale = log10,
    xticks = nlist,
    xlabel = "n",
    title = "Relative error",
)
scatterlines!(ax, nlist, e; label = "Data")
lines!(ax, collect(extrema(nlist)), n -> n^-2.0; linestyle = :dash, label = "n^-2")
axislegend(ax)
fig

save(joinpath(outdir, "convergence.png"), fig)

---

This page was generated using Literate.jl.